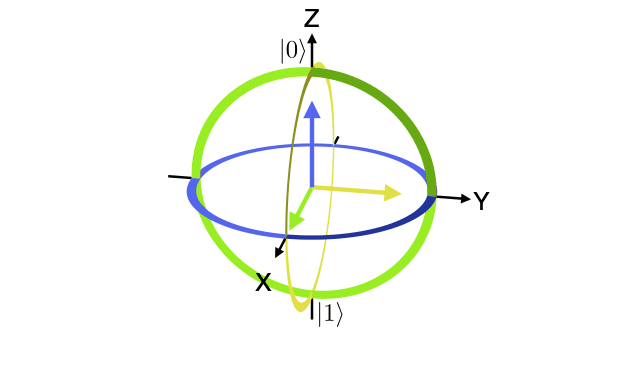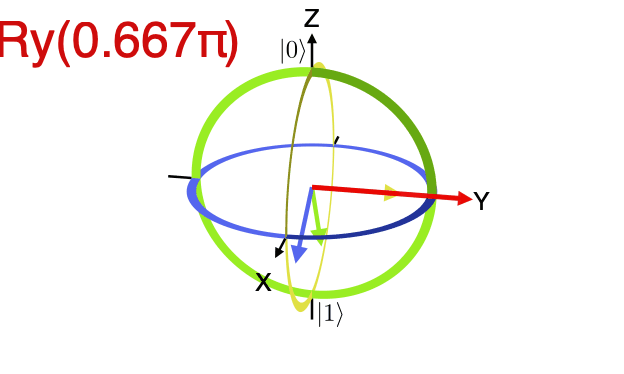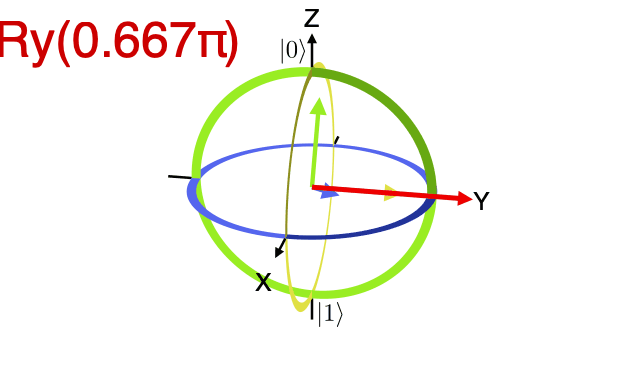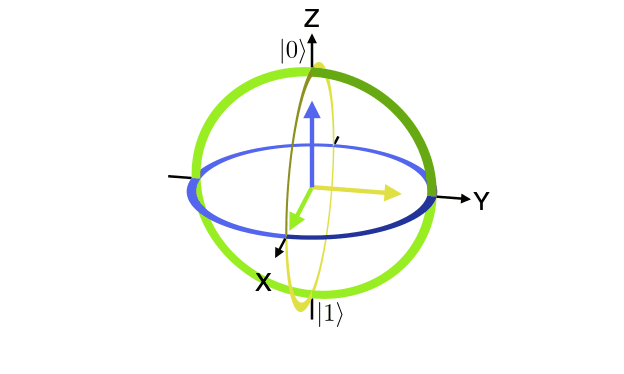
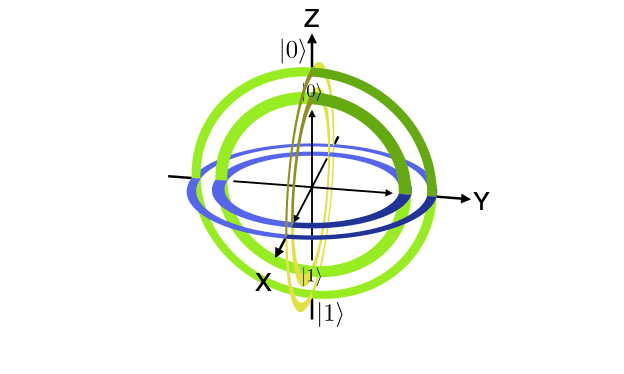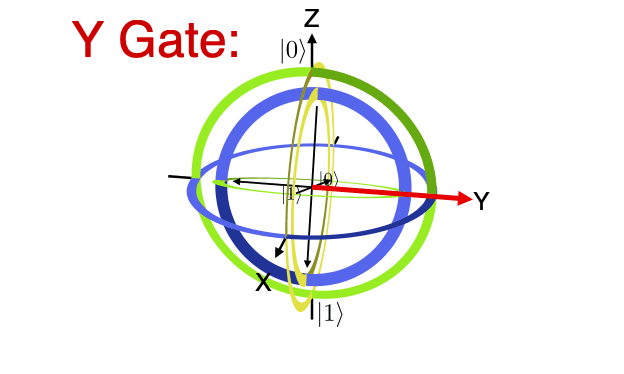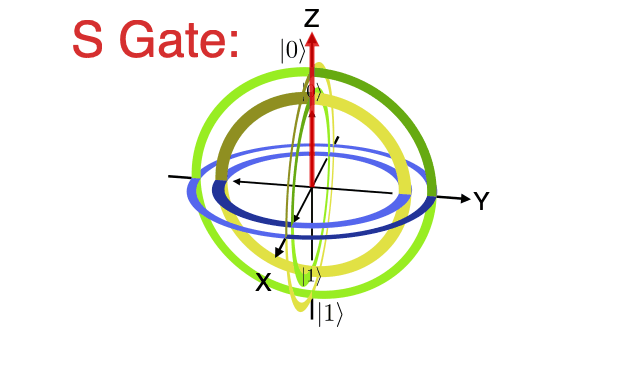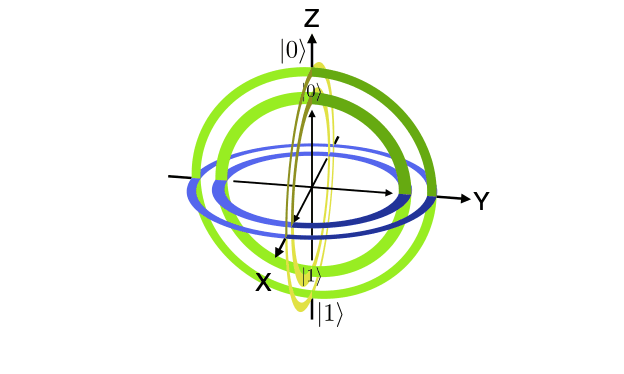
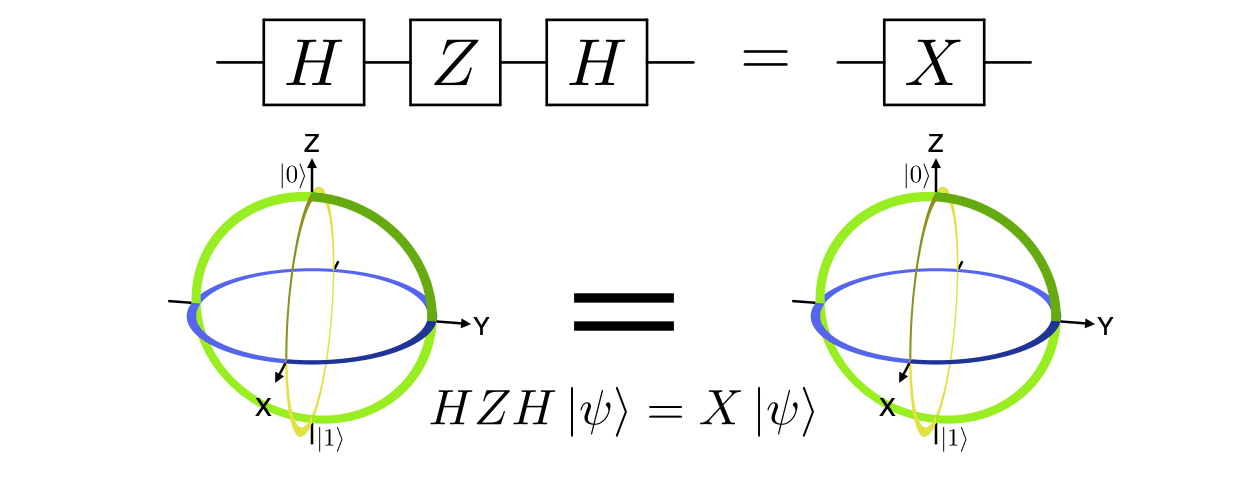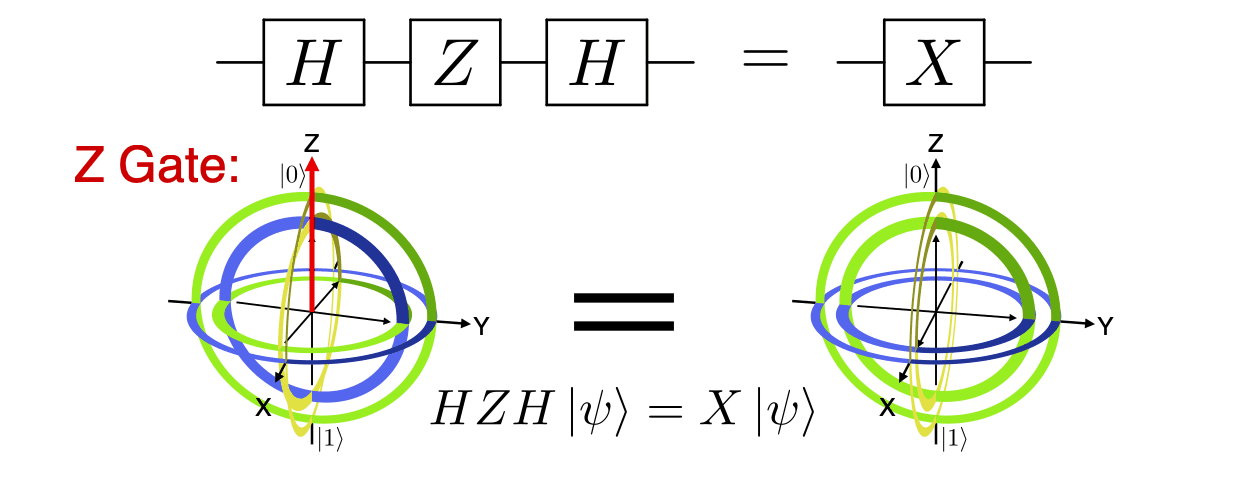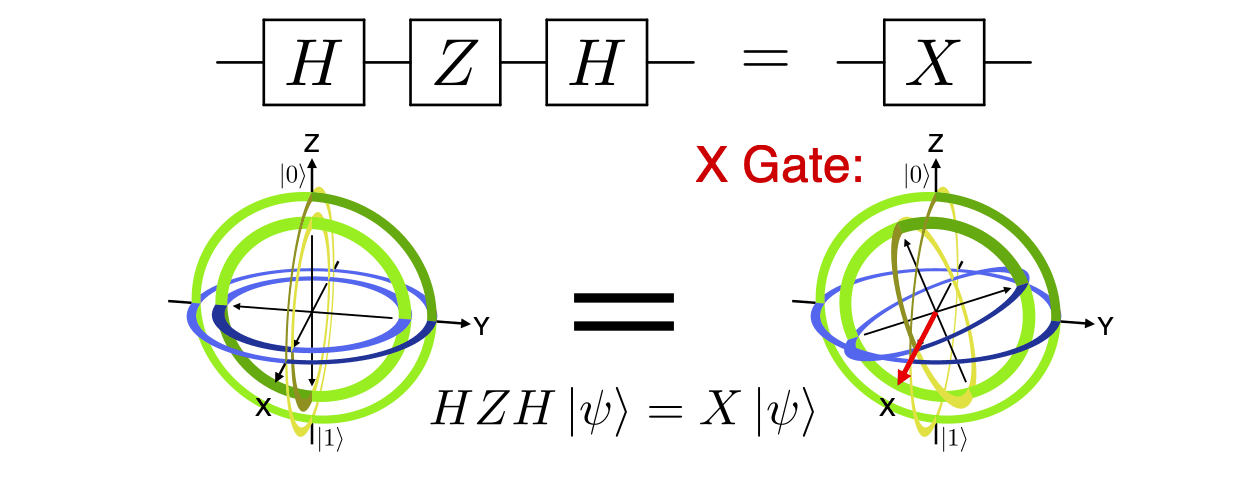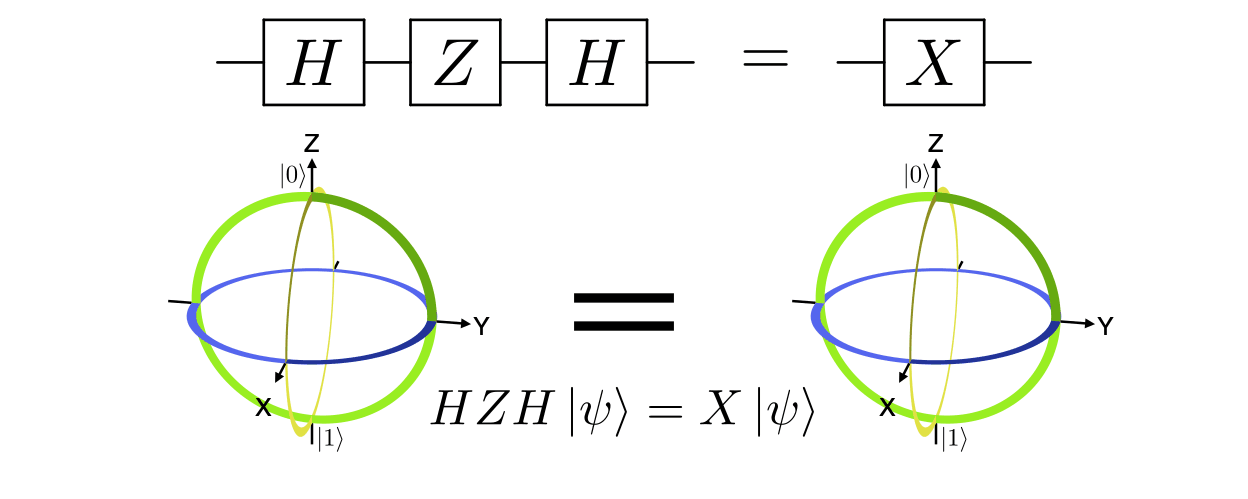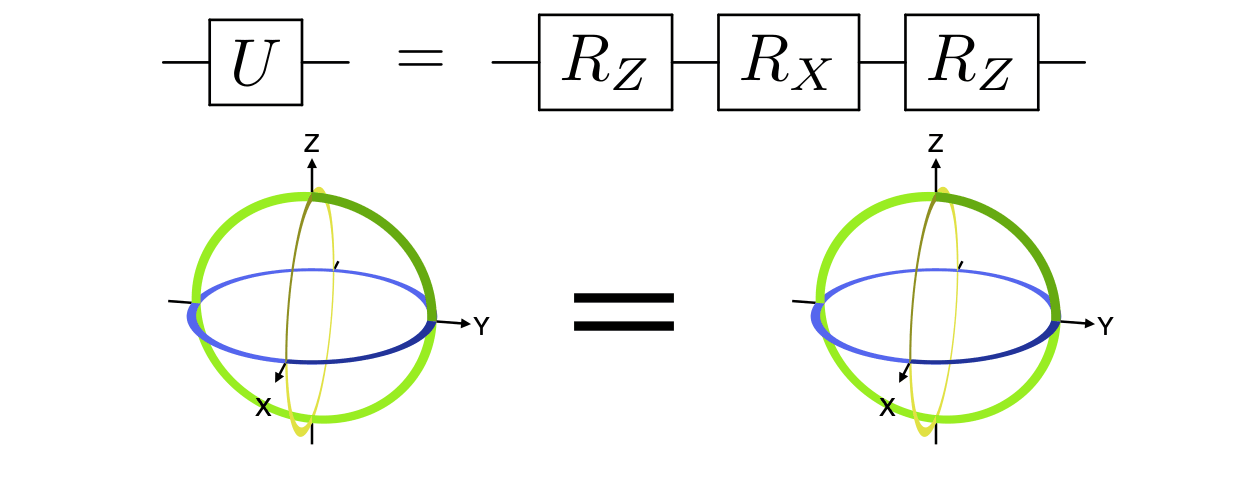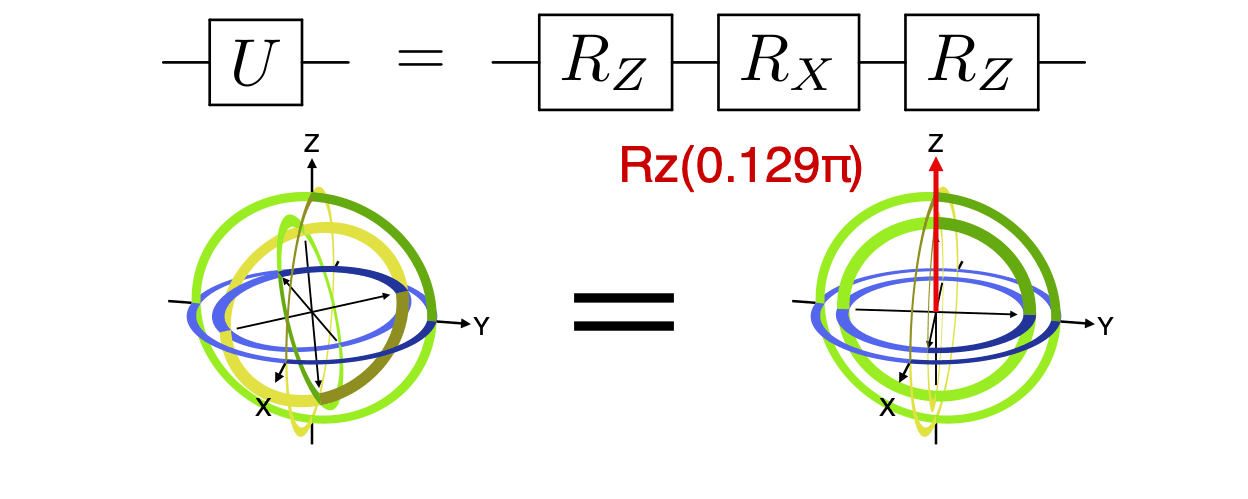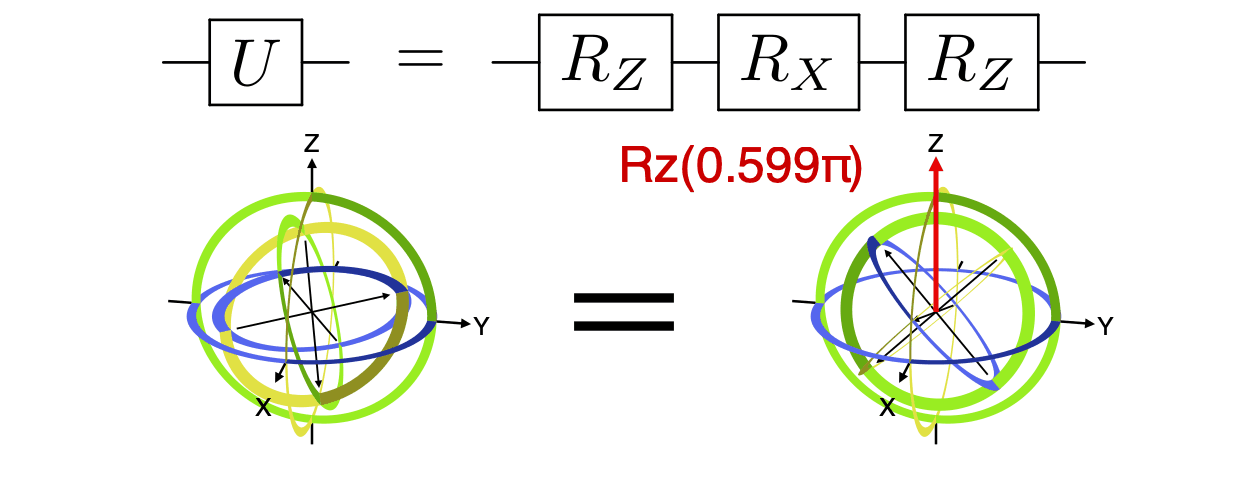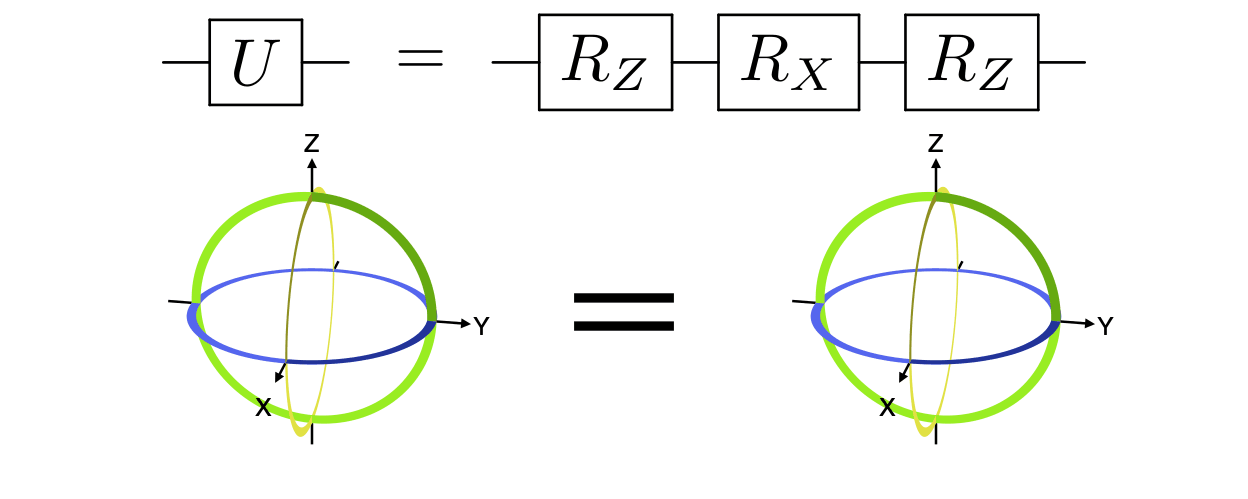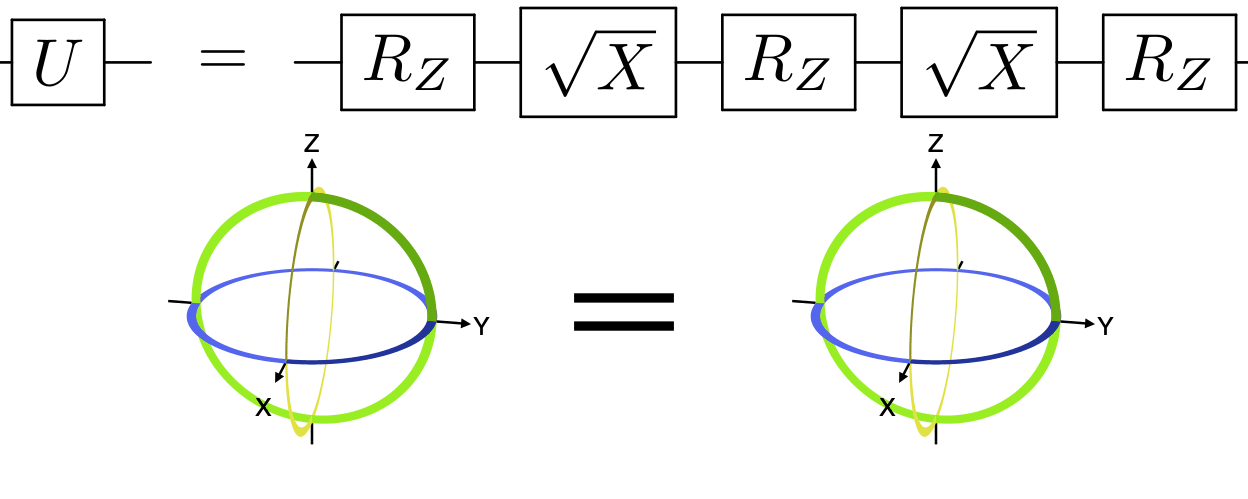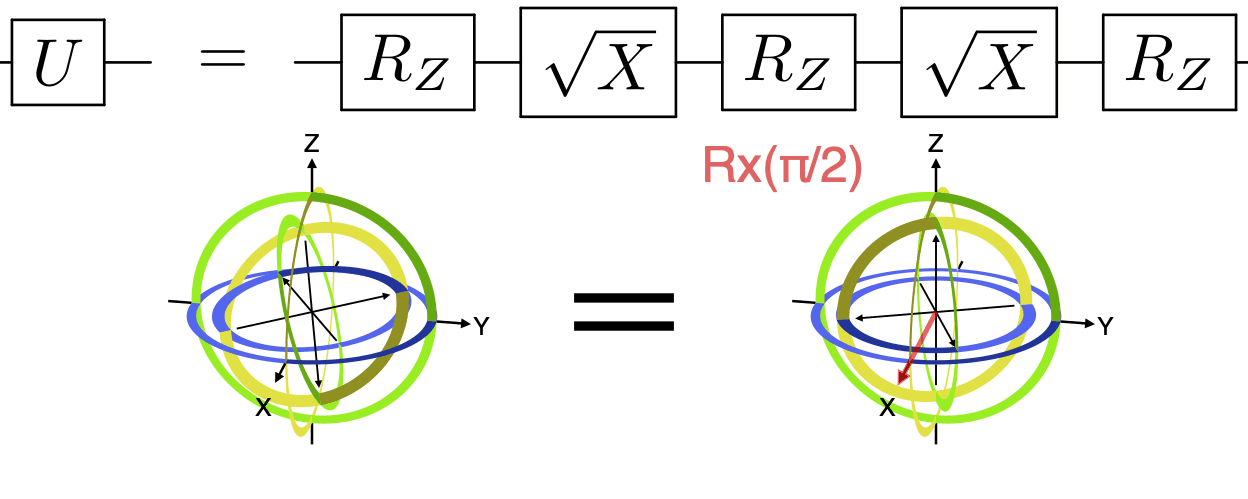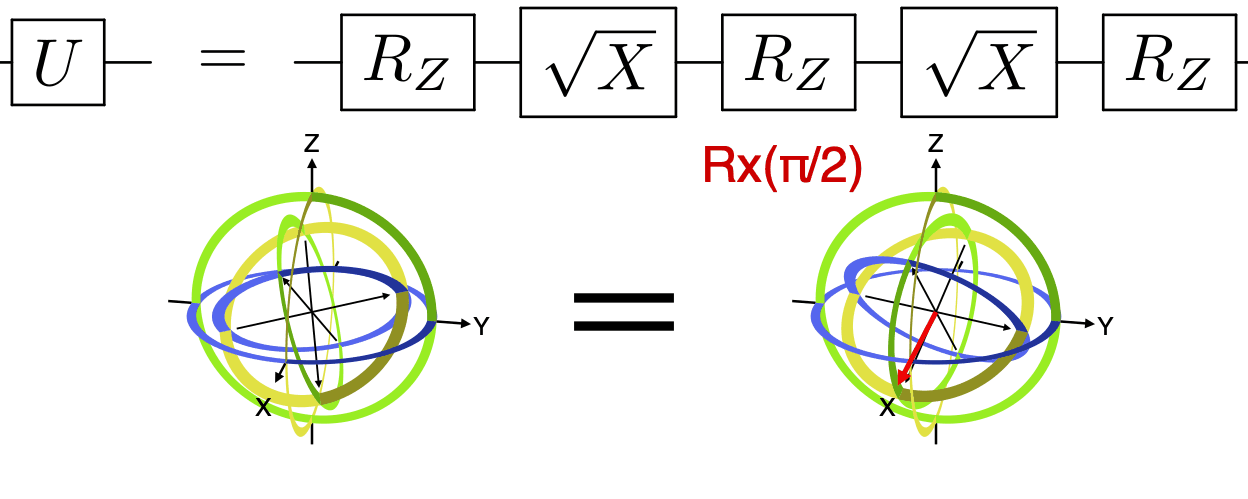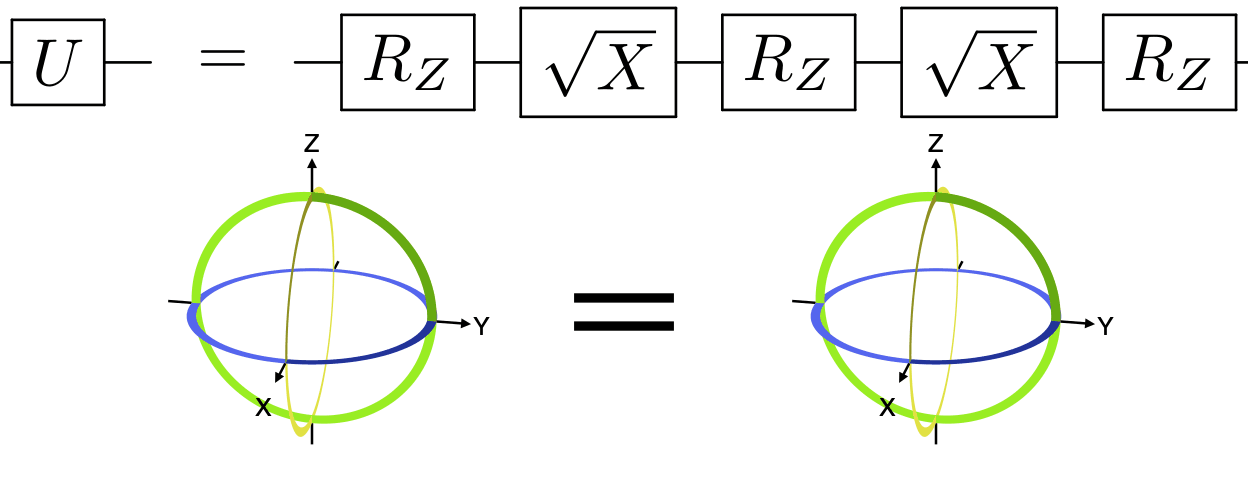A collection of visualization tools for the qubit Bloch sphere. The Bloch sphere is a useful representation of the state of a single-qubit quantum computer.
See also: Feynman path integral visualization
bloch_sphere is available on PyPI:
python3 -m pip install bloch_sphereCairo needs to be installed separately to render videos. See platform-specific instructions for Linux, Windows, and macOS from Cairo. Below are some examples for installing Cairo on Linux distributions and macOS.
Ubuntu
sudo apt-get install libcairo2macOS
Using homebrew:
brew install cairoThis package provides a command line tool to generate animations.
In your shell, run the following (run animate_bloch -h for help).
animate_bloch hadamard x y s sanimate_bloch2 xy_vs_z x,y zWith annotations:
animate_bloch2 xy_vs_z_annotated \
x,y z \
--circuit '& \gate{X} & \gate{Y} & \qw & \push{=} & & \gate{Z} & \qw' \
--equation '$YX\ket{\psi}=Z\ket{\psi}$' \
--fps 20 \
--mp4Custom gates: custom;<x-axis>;<y-axis>;<z-axis>;<number half rotations>;<label>
animate_bloch2 custom_hzy "custom;0;1;1;1;Hzy" "s,h,inv_s"Alternate drawing styles:
animate_bloch ry_gate_arrows --style arrows ry,0.666667 ry,0.666667 ry,0.666667from bloch_sphere.animate_bloch import do_or_save_animation, AnimState
@do_or_save_animation('my_animation', save=False, fps=20, preview=True)
# Or
#@do_or_save_animation('my_animation', save='gif', fps=20, preview=True)
#@do_or_save_animation('my_animation', save='mp4', fps=20, preview=False)
def animate(state: AnimState):
state.x_gate()
state.y_gate()
state.s_gate()
state.s_gate()
...
state.wait() # Pause at the endfrom bloch_sphere.animate_bloch_compare import main
main('hzh_x', 'h,z,h'.split(','), 'x'.split(','),
r'& \gate{H} & \gate{Z} & \gate{H} & \qw & \push{=} & & \gate{X} & \qw',
r'$HZH\ket{\psi}=X\ket{\psi}$',
mp4=False,
fps=20,
preview=True,
)Or
import drawSvg as draw
import latextools
from bloch_sphere.animate_bloch_compare import render_animation
# Add some extra labels
zero_ket = draw.Group()
zero_ket.draw(latextools.render_snippet('$\ket{0}$', latextools.pkg.qcircuit),
x=0, y=0, center=True, scale=0.015)
one_ket = draw.Group()
one_ket.draw(latextools.render_snippet('$\ket{1}$', latextools.pkg.qcircuit),
x=0, y=0, center=True, scale=0.015)
zero_ket_inner = draw.Use(zero_ket, 0, 0, transform='scale(0.75)')
one_ket_inner = draw.Use(one_ket, 0, 0, transform='scale(0.75)')
w = 624*2 # Output width
fps = 20
draw_args = dict(
w = w/2,
outer_labels=[
[(0, 0, 1), (-0.15, 0.13), zero_ket],
[(0, 0, -1), (0.15, -0.13), one_ket],
],
inner_labels=[
[(0, 0, 0.8), (0, 0), zero_ket_inner],
[(0, 0, -0.8), (0, 0), one_ket_inner],
],
)
gates1 = 'h,z,h'.split(',')
gates2 = 'x'.split(',')
def func1(state):
state.draw_args = dict(draw_args)
state.draw_args['inner_labels'] = []
state.sphere_fade_in()
state.apply_gate_list(gates1, final_wait=False)
state.wait()
for _ in gates2:
state.i_gate()
state.wait()
state.wait()
state.sphere_fade_out()
state.wait()
def func2(state):
state.draw_args = dict(draw_args)
state.draw_args['inner_labels'] = []
state.sphere_fade_in()
for _ in gates1:
state.i_gate()
state.wait()
state.apply_gate_list(gates2, final_wait=False)
state.wait()
state.wait()
state.sphere_fade_out()
state.wait()
render_animation('hzh_x_compare', func1, func2,
r'& \gate{H} & \gate{Z} & \gate{H} & \qw & \push{=} & & \gate{X} & \qw',
r'$HZH\ket{\psi}=X\ket{\psi}$',
save='gif', # False, 'gif', or 'mp4'
fps=fps,
preview=True,
w=w)Any single-qubit gate can be decomposed into a series of three rotations about fixed axes, most commonly as rotations about Z, X, and Z. See the example code that generated the below animation.
Any single-qubit gate can also be decomposed into a series of three Z rotations with fixed X rotations of π/2 (1/4 turn) in between. See the example code that generated the below animation.