Fibonacci Sequence

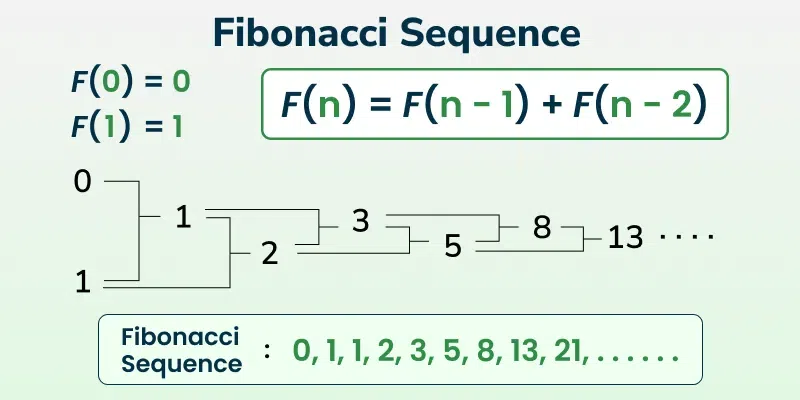
The Fibonacci Sequence is a series of numbers starting with 0 and 1, where each succeeding number is the sum of the two preceding numbers. The sequence goes on infinitely.
So, the sequence begins as:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Fibonacci Sequence

History of the Fibonacci Sequence

The Fibonacci sequence is named after Leonardo of Pisa, who is more commonly known as Fibonacci. He was an Italian mathematician born around 1170 and died around 1250.

Fibonacci introduced the sequence to Western mathematics in his book “Liber Abaci” (The Book of Calculation), published in 1202. In “Liber Abaci”, Fibonacci posed a problem involving the growth of a population of rabbits. The problem was stated as follows:

Suppose a pair of rabbits is placed in an enclosed area. How many pairs of rabbits will be produced in one year if every month each pair produces a new pair that becomes productive from the second month on?

This problem led to the formation of the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, . . .

Fibonacci Sequence Formula

The Fibonacci formula is used to find the nth term of the sequence when its first and second terms are given.

The nth term of the Fibonacci Sequence is represented as F_n. It is given by the following recursive formula,

F_n = F_n-1 + F_n-2

where,

• n > 1
• The first term is 0 i.e., F₀ = 0
• The second term is 1 i.e., F₁ = 1

Using this formula, we can easily find the various terms of the Fibonacci Sequence. Suppose we have to find the 3rd term of this Sequence then we would require the 2nd and the 1st term according to the given formula, then the 3rd term is calculated as,

• The F₃ = F₂ + F₁ = 1 + 1 = 2

Thus, the third term in the Fibonacci Sequence is 1, and similarly, the next terms of the sequence can also be found as,

• F₄ = F₃ + F₂ = 2 + 1 = 3
• F₅ = F₄ + F₃ = 3 + 2 = 5

and so on.

Below are the first 10 Fibonacci numbers in the sequence List.

• Fibonacci Sequences have infinite terms.
• By closely observing the table we can say that F_n = F_n-1 + F_n-2 for every n > 1.

Note: The Fibonacci Sequence can start in two ways:

• 0 and 1: This is the most common convention, where the sequence begins as 0, 1, 1, 2, 3, 5, 8, 13, …
• 1 and 1: In some contexts, the sequence starts with 1, 1, 2, 3, 5, 8, 13, …

Fibonacci Sequence in Nature

Many natural patterns follow a spiral structure that aligns with Fibonacci numbers:

• Sunflowers: The number of spirals in the center of a sunflower often corresponds to Fibonacci numbers.
• Pinecones: The scales of a pinecone form spiral patterns that match Fibonacci numbers.
• Shells (Nautilus, Snails, etc.): Their growth follows a logarithmic spiral, which is closely related to the Fibonacci sequence.
• Galaxies: Many spiral galaxies, such as the Milky Way, follow Fibonacci-like spirals.

These spirals are examples of logarithmic spirals, which maintain the same shape as they expand.

Read More: Fibonacci Sequence in Real-Life

Properties of the Fibonacci Sequence

Important properties of the Fibonacci Sequence are:

• We can easily calculate the Fibonacci Numbers using the Binet Formula:

F_n = (Φⁿ – (1-Φ)ⁿ)/√5

Using this formula we can easily calculate the n^th term of the Fibonacci sequence as, for finding the fourth term of the Fibonacci sequence,

F₄ = (Φ⁴ – (1-Φ)⁴)/√5 = ({1.618034}⁴– (1-1.618034)⁴)/√5 = 3

• For larger terms, the ratio of two consecutive terms of the Fibonacci Sequence converges to the Golden Ratio.

• Multiplying a term of the Fibonacci Sequence with the Golden Ratio gives the next term of the Fibonacci sequence as,

F₇ in the Fibonacci Sequence is 13 then F₈ is calculated as,

F(n)=F(n−1)+F(n−2)

F(8) = F(7) + F(6)
F(8) = 13 + 8 = 21
Thus, the F₈ in the Fibonacci Sequence is 21.

• We can also calculate the Fibonacci Sequence for below zero numbers as,

F_-n = (-1)ⁿ⁺¹F_n

For example, F_-2 = (-1)²⁺¹F₂ = -1

• Fibonacci Numbers are used to define other mathematical concepts such as Pascal Triangle and Lucas Number.

Golden Ratio and Fibonacci Sequence

The golden ratio (Φ) is a special mathematical constant approximately equal to 1.618. It is often represented by the Greek letter phi (Φ) and is also known as the golden number, golden proportion, or the divine proportion.

Formula:

Φ = F_n/F_n-1

As you divide two consecutive terms in the Fibonacci sequence, the resulting ratio approaches the golden ratio. The ratio gets closer to 1.6180339887 as the Fibonacci numbers increase.

• X-axis: The ratio F(n+1)/F(n)​, where F(n) denotes the Fibonacci number at position n.
• Y-axis: The value of the ratio for each Fibonacci pair.

Fibonacci & Golden Ratio

As you move along the x-axis, the value of the ratio F(n+1)/F(n)​ gets closer to the golden ratio, Φ. This relationship is a visual representation of how Fibonacci numbers converge to this constant as the sequence progresses.

Read More,

• Interesting Facts about Fiboonacci Numbers
• Arithmetic Progression
• Geometric Progression
• Sequences and Series

Interesting Problems Based on the Fibonacci Sequence

• Climbing Staircase to reach the top: There are n stairs, and a person standing at the bottom wants to climb stairs to reach the top. The person can climb either 1 stair or 2 stairs at a time, the task is to count the number of ways that a person can reach at the top.

• Dudeney’s Cow Problem: Cows in FooLand are interesting animals. One of their specialties is related to producing offspring. A cow in FooLand produces its first calve (female calf) at the age of two years and proceeds to produce other calves (one female calf a year).

GeeksforGeeks

Improve

Article Tags :

• Mathematics
• School Learning
• Math-Concepts
• Sequence and Series